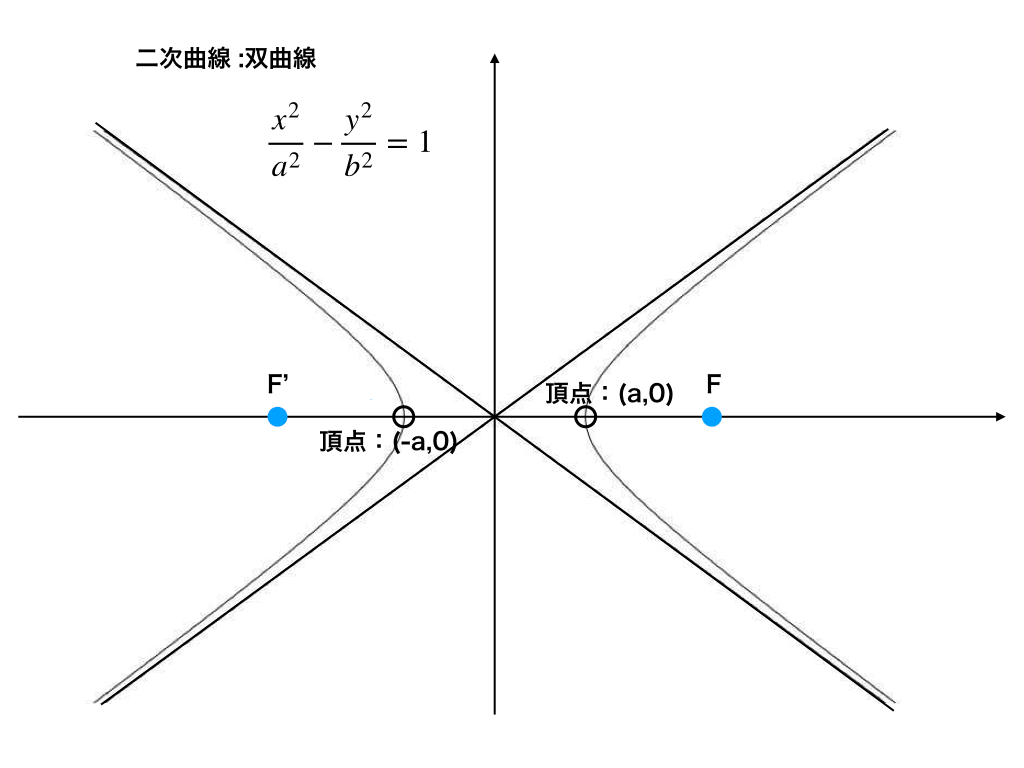
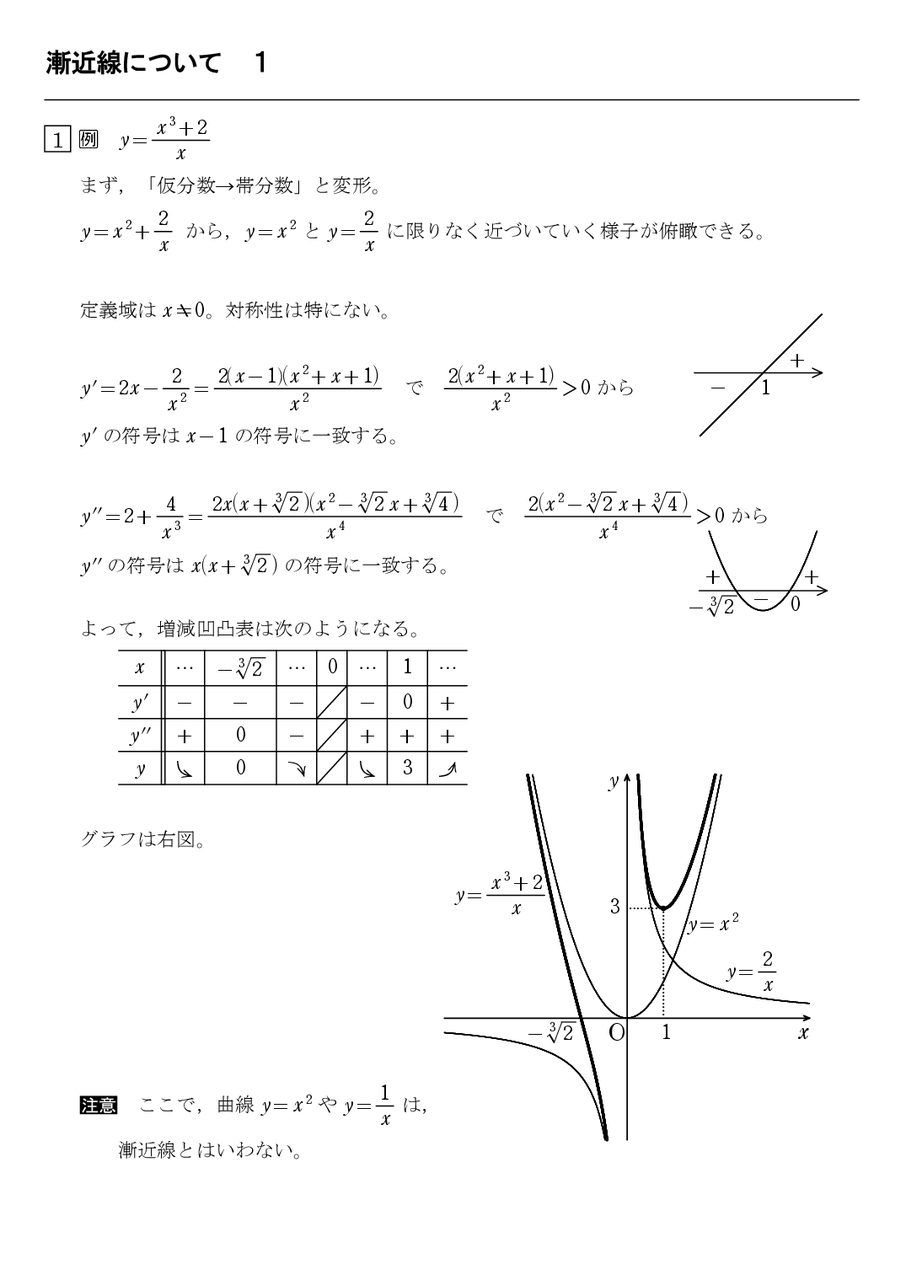
漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、 · 解2問題文の式を変形して漸近線を求める 原点を通るからx=0,y=0を代入するとb=0 \(\displaystyle \frac{ax}{3xc}=\frac{a}{3}\frac{ac}{3(3xc)} = \frac{a}{3} – \frac{\frac{ac}{9}}{x\frac{c}{3}} \) よって 漸近線は\(\displaystyle x=\frac{c}{3} \)と\(\displaystyle y=\frac{a}{3} \) よってc=6,a=12 · 双曲線について x^2/a^2y^2/b^2=1 焦点の座標を(c,0)(c,0) 漸近線;y=bx/a だとします。 c=√(a^2b^2)となるのは何故でしょうか? 手元にはグラフがあるのですが、これが導けません・・。 よろしくお願い致します。
双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説
数3 微分 グラフ 漸近線 求め方
数3 微分 グラフ 漸近線 求め方-② y=f(x)は直線x=1を漸近線として、点(2,3)を通る。 解) しかし、前述の方法ではkの値が分数になると計算が面倒になり、結果はまた計算力に頼る形になってしまうことがある。たとえば、 ex2) 分数関数 の逆関数を求めよ。 解) 漸近線は 。今日は漸近線の求め方について解説します。 漸近線とは曲線が近づく直線のことで 漸近線には3種類あります! ①x軸に平行な漸近線 x→±∞のとき, f(x)→αとなる極限値が存在するとき,,y=αが漸近線となる。 ②y軸に平行な漸近線
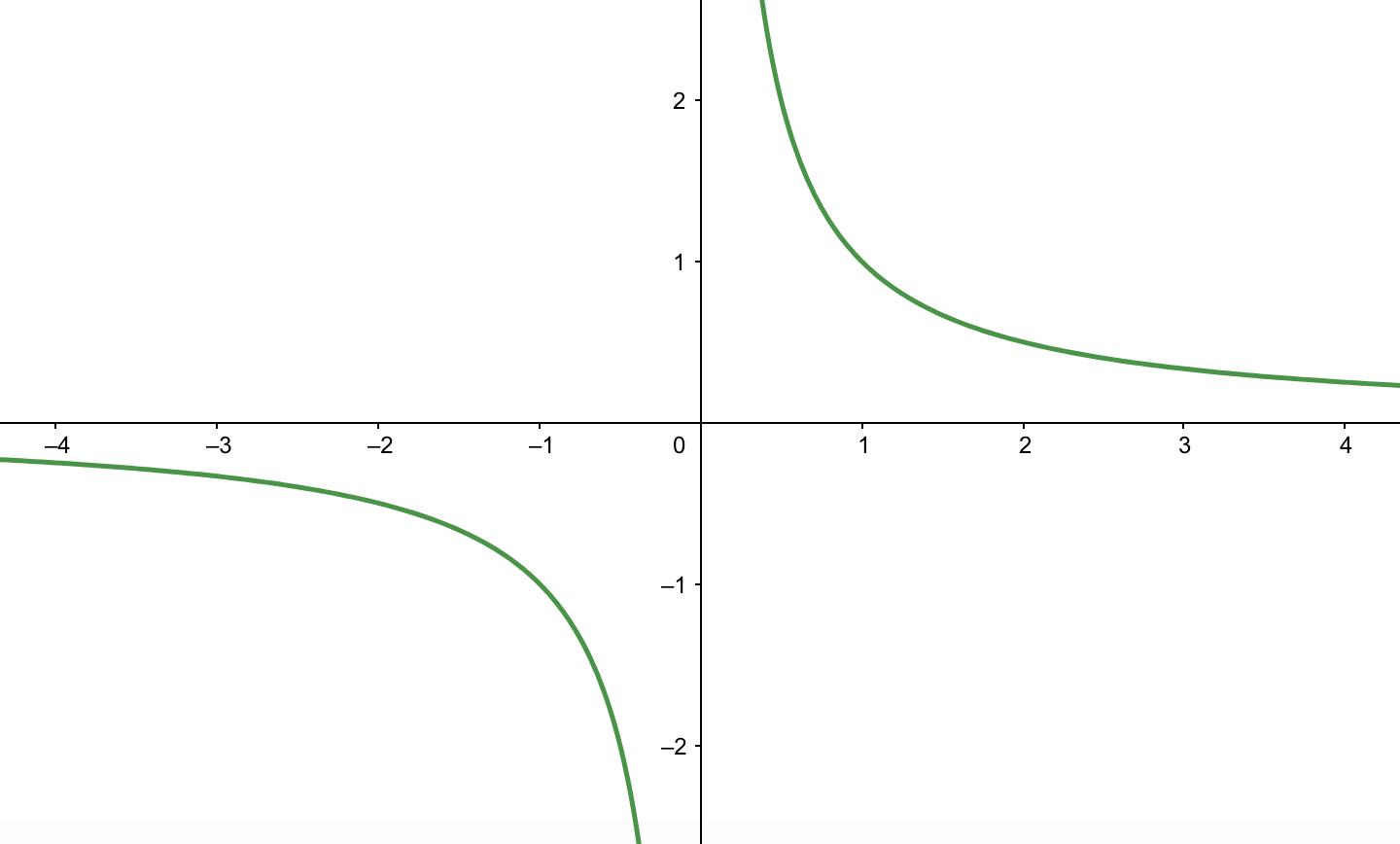



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
· 1 回答 数Ⅲの関数のグラフで、漸近線の求め方が全然わかりません。 チャート読んでも分からんかったのでどなたか分かりやすく解説おねがいします。 関数はy=x√ (1x)の漸近線の求め方も付けていただ 数Ⅲの関数のグラフで、漸近線の求め方が全然わかりません。 チャート読んでも分からんかったのでどなたか分かりやすく解説おねがいします。 関数 · lim θ → 0 sin θ θ = 1 \displaystyle\lim_ {\theta\to 0}\dfrac {\sin\theta} {\theta}=1 θ→0lim θsinθ = 1 ・関数の連続性 →関数の右極限,左極限と連続性 ・区間,閉区間,開区間数3の微分の応用のところの漸近線の求め方がわかりません。 写真の問題にかかわらず、なにをしているのかすらわかりません。 また、第二次導関数はどんな時に使用するのでしょうか? めんどくさい質問をすみません。
数Ⅲaxbという漸近線の求め方 質問があればこちらからどうぞ 記事を科目別・教科書順にまとめたページはこちら いままで全ッ然分からなかった漸化式が この記事を読んでスッと分かりました!ほんとにありがとうございます! 題名の通りですが、漸近線の求め方の公式について質問閲覧数1702 関数のグラフの概形を書く手順を教えてください。 特に1:増減表の形 2:漸近線の求め方と漸近線を求める位置 をお願いします。 ベストアンサー 数学・算数; · 漸近線を見出すことは、曲線の概形をつかむ一助となる。 特に、座標平面における関数に対しては、そのグラフの漸近線の方程式は(存在の可否も含めて)求め方が確立されている。関数のグラフの接線の極限が存在するならばそれは漸近線に等しい 。
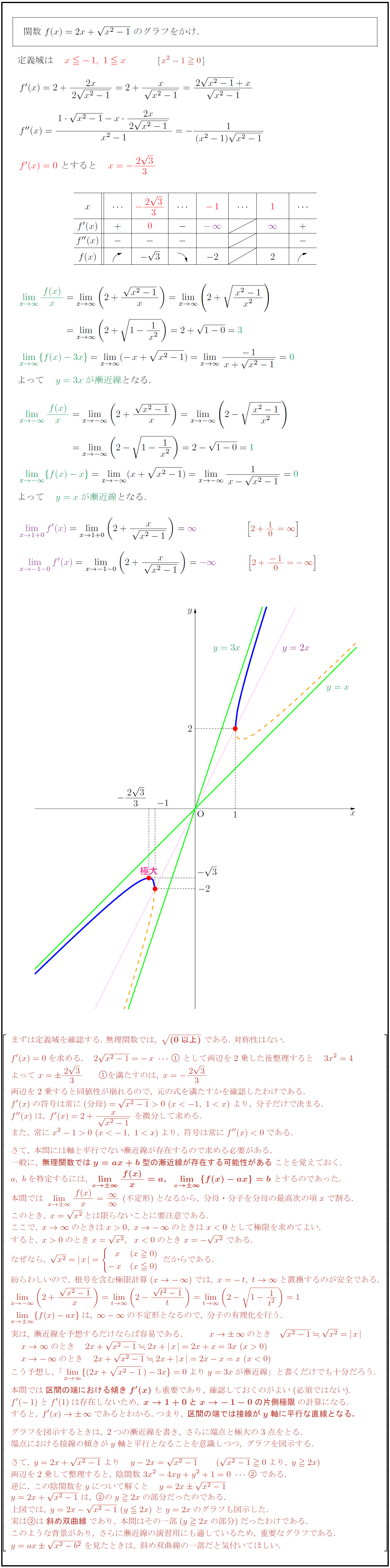
· 漸近線 媒介変数表示された曲線の漸近線 (sec(t), cosec(t)) は、水平方向と垂直方向にそれぞれ2本ずつ漸近線を持つ。この曲線は x2 y2 = (xy)2 と陰関数表示できる。媒介変数表示 · C;4 xy^238 y357=0 高1までに學ぶ 易しい 放物線 を定める。 F(x,y)=((4/(4 x2 y^238 y)),(2 y38)/(4 x2 y^238 y))なる 非線型写像による C の像を 多様な発想で 求めて もし Fが 双曲線なら 漸近線を多様な発想で求めて F と共に図示し 共軛な双曲線をも 図示願います; 不定方程式 の解集合 F∩Z^2 の · 漸近線の基本的な求め方は、1、y軸に平衡な漸近線、2、y軸に平衡でない漸近線、とあります。 これを使って 問題1、y=(x^2x1)/(x1)の漸近線を求めよ。 問題2、y=2x(x^21)^(1/2)の漸近線を求めよ。 です。 解答は、問題1では式を変形して、漸近線を予想して、解いています。問題2では、明らかに、y軸に平行な漸近線はない、として、y軸に平行でない漸近線を




漸近線 説明編 数 微分法 現大手予備校講師の5分でわかる 高校数学 Youtube



増減凹凸表を書く手順 7 漸近線 1 怜悧玲瓏 高校数学を天空から俯瞰する
まとめ よりリアルな(凹凸まで調べた)グラフを描くためには、 を求め、 増減表を描き、 の符号から曲がり方を判断すれば良い。 最後に漸近線チェックを行う。 結局、新しい知識は何もなくて、 ただ曲がり方を調べてね って話です。 この曲がり方 · 2次曲線 12 xx^24 y8 x y4 y^2=0 の漸近線を求めてみました。 y=t1(x1/3)1/6, y=t2(x1/3)1/6 t1=1Sqrt3/2 t2=1Sqrt3/2 Mathematica は大抵のことは期待以上の計算をしてくれますが、分母の有理化は苦手のようです。 所々、手計算を併用しました。漸近線の式が思ったよ · (e^2x1) / (e^x2) の漸近線を求めよという問題があります。xはわかったのですが、 y軸と平行な漸近線の求め方がわかりません。答えは y= 1/2のようです。解き方を、教えてください。 xy平面上において、y軸と平行な漸近線を求め




高校数学 分数関数のグラフ 1 映像授業のtry It トライイット




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどういう意味な Clear
・三角関数のグラフの概形と書き方高校数学Ⅲ ・漸近線とは?求め方高校数学Ⅲ ・複雑な関数の概形(偶関数と奇関数)高校数学Ⅲ 37方程式、不等式への応用 ・実数解の個数の求め方高校数学Ⅲ ・不等式の証明の仕方高校数学Ⅲ · 2 x 3 2x3 2 x 3 を x 1 x1 x 1 で割ると, 2 x 3 = 2 (x 1) 1 2x3=2(x1)1 2 x 3 = 2 (x 1) 1 となるので,基本形は, y = 2 1 x 1 y=2\dfrac{1}{x1} y = 2 x 1 1 ,つまり y − 2 = 1 x 1 y2=\dfrac{1}{x1} y − 2 = x 1 1 となる。 · $x^22x$ において $x$ に $1$ を代入すると、$3$ になるので+の値です。あとは $x=2$ で極値をとるので、それの右側の $x=3$ あたりで考えます。そうすると $ 3^22\times3=3$ となり+の値となります。 これで増減表の $f'(x)$ の部分は完成です。 次に $f"(x)$ を考えます。$\displaystyle y"=\frac{2}{(x1)^3}$ は分母が+になる場合とーになる場合があるので気を付けま




増減表 凹凸表 で変曲点を調べて三角関数のグラフを書こう 2回微分 数 遊ぶ数学
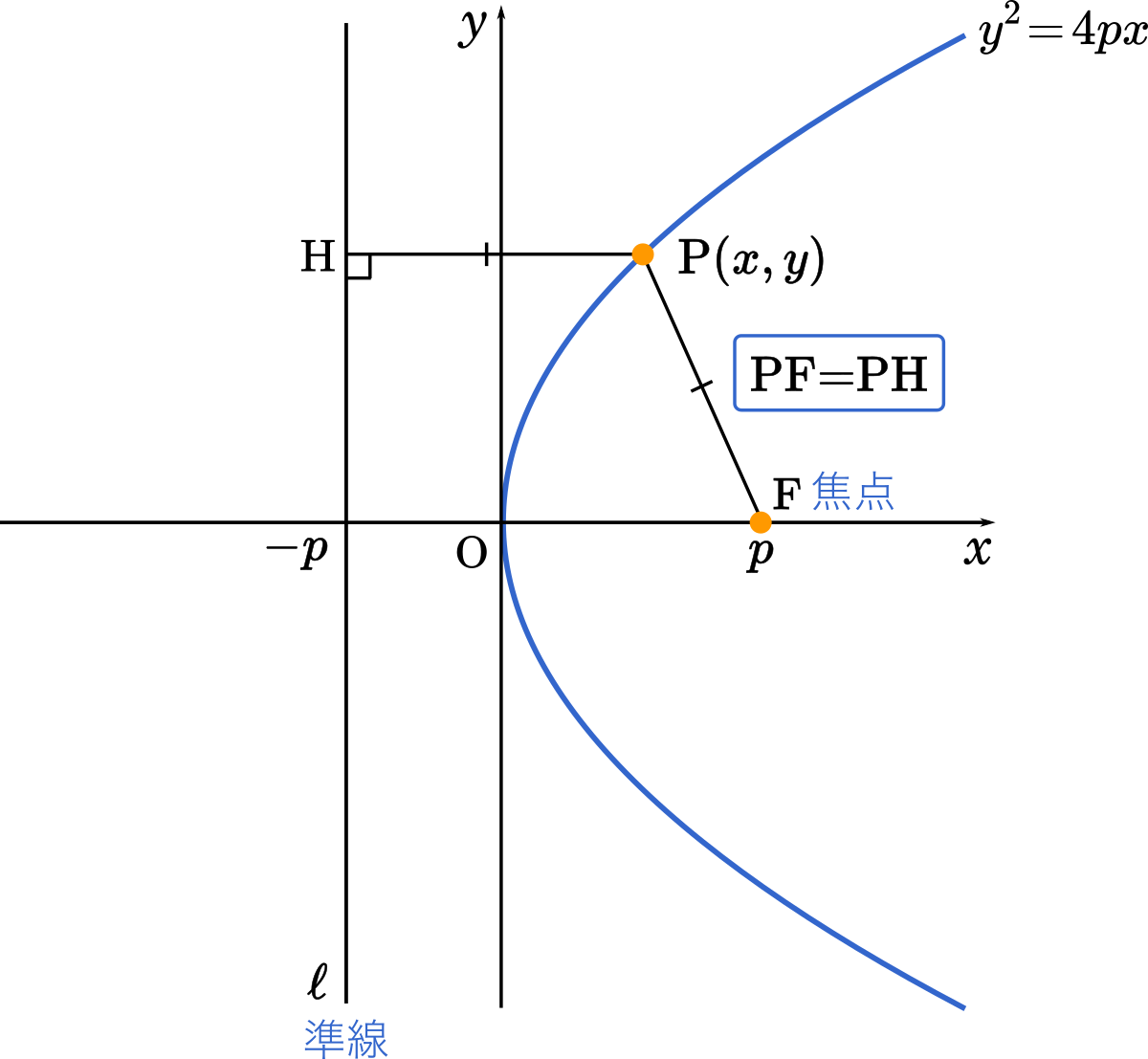



北海道大16理系第5問 数iibベクトル 数iii放物線 直線に下ろした垂線との交点 放物線の焦点と準線を求める Mm参考書
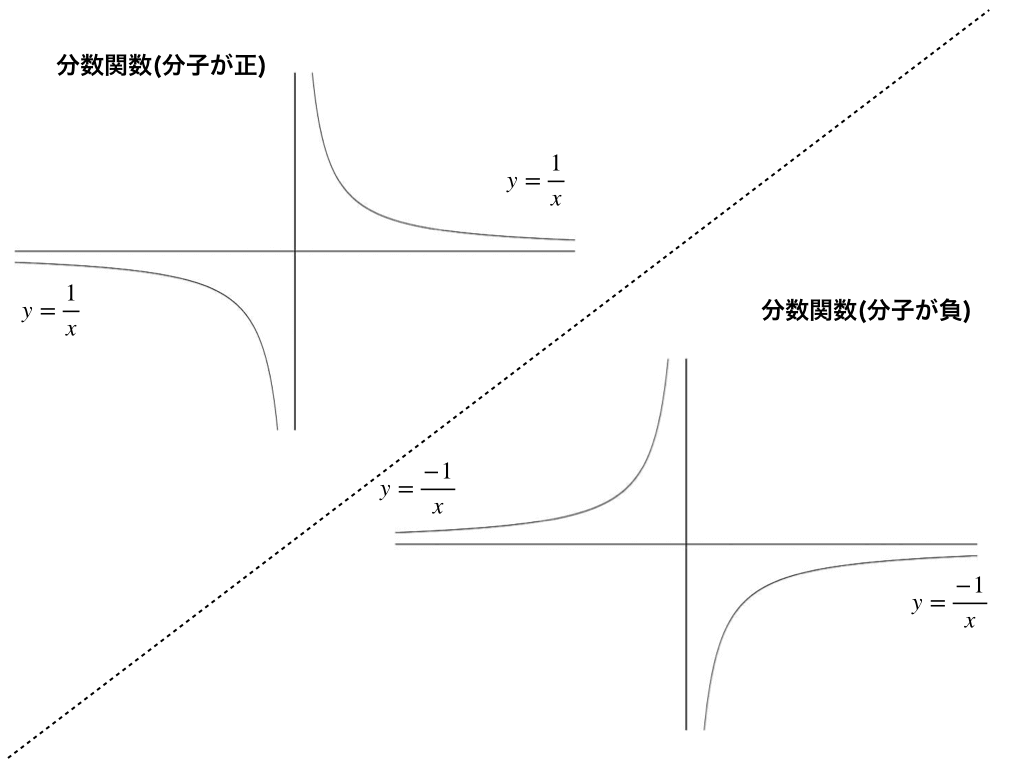
· ここでは陽関数y=f(x)の形のグラフの書き方をお教えします。 基本手順 1 定義域を確認!(logの真数条件や分母=0になる点の除外など) 2 増減(f'(x)=0を計算) 3 凹凸(問題文に調べなくてもいいと書かれている場合は除く。f"(x)=0を計算) 4 漸近線 (主にx軸,y軸に平行なものを調べる。4 漸近線の有無の判別方法 41 チェック① \(y\)軸に平行でない漸近線があるか · さらに、平行移動を考えると、y=(分数)+3なので、\(\frac{\pm k}{x}\)のグラフに比べて、"3"だけy軸正方向へ動きます。 ここで、もう一つの漸近線は「y=3」であることがこの式変形によってわかりました。 <答えのグラフ> 無理関数とは?




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書
小野測器減衰をあらわす係数の意味と求め方 (page2) 3 減衰の効果 ここまでは、振幅が指数関数的に減衰していく状態を前提に減衰比や損失係数の求め方について説明しましたが、ここからは減衰比が実際の振動で物理的にどのような意味を持つかについて回答 ルーシー 2年弱前 そのやり方是非、頭に入れておいたほうがいいですよ。 lim x→∞ f (x)/x=a (aは傾きになる) lim x→∞ (f (x)−a)=b (bは切片になる) ゆえにf (x)の漸近線はy=ax+b 僕の高校時代のとても理屈を大切にしていた数学の教師でもこの理屈は言わずにこの漸近線の求め方を覚えろと言われました (もしくは漸近線をかけという記述がなければ求める必要が · 計算量オーダーの求め方を総整理! 〜 どこから log が出て来るか 〜 NTT データ数理システム でリサーチャーをしている大槻 (通称、けんちょん) です。 今回は計算量オーダーの求め方について書きます。 0 はじめに 世の中の様々なシステムや




この漸近線の求め方がわかりません なぜy Xをするのか教えて下さい Clear




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
· 3333 (グラフの準備:漸近線の求め方 (無理関数)) 2 2,718 ビュー このページを評価 (6 投票) 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組み · 今回も宜しくお願い致します。 今回は問題ではなく、私自身の疑問についてなのですが、数IIIのグラフを描く際に求める漸近線についてです。 f (x)= (x3) {1/ (x2)} という形に変形させて、漸近線はy=x3とx=2だと求められると思います。 そこで質問なのです3 漸近線の求め方 31 \(y\)軸に平行な漸近線の求め方;




漸近 線 求め 方 漸近線の求め方を解説しました



曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋
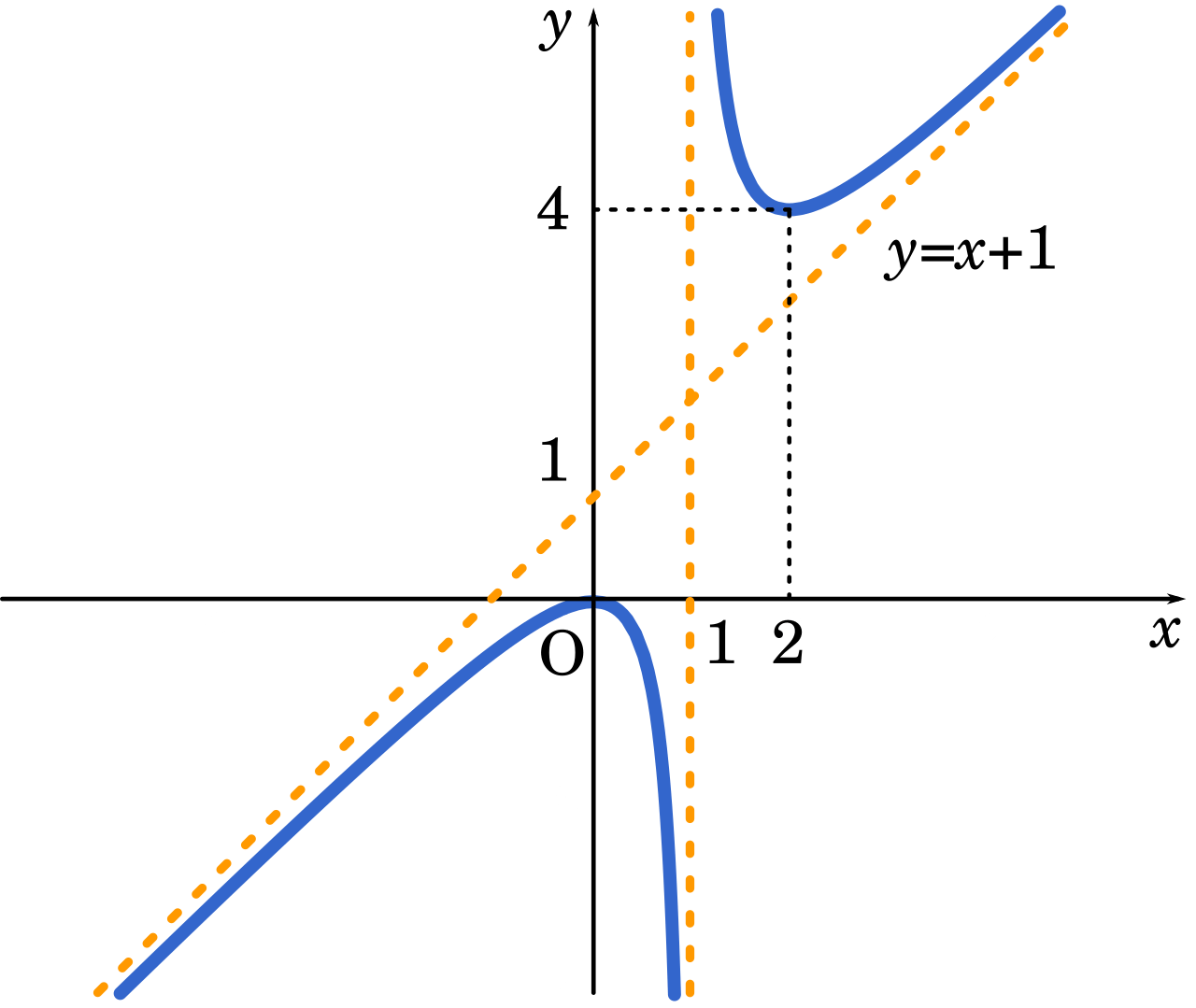
· 中学数学で習う反比例。 基礎の基礎ではありますが、グラフの描き方や式の求め方など、意外と忘れがちなところが多いのも事実です。 また、高校数学で習う「分数関数」はこの反比例がわかっていることを前提に進むので、反比例の理解があやふやなままだと分数関数まで苦手になってX が負の無限大に接近する場合の極限もまた 3 になります。この結果は、 y = 3 のラインが、 f の水平方向の漸近線であることを意味しています。 f の垂直方向の漸近線を求めるには、分母を 0 に等しくなるように設定して、それを解きます。→「縦」の漸近線の方程式は x = 2 および x = 4 です。 (x = 1 , x = 3 は漸近線ではなく,x軸との交点です.) (B) 「斜め又は横」の漸近線 x → ∞ のとき y = axb が漸近線であるとは, {f(x) (axb)} = 0 ・・・(1) となることです。



漸近 線 求め 方 漸近線の求め方を解説しました



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典
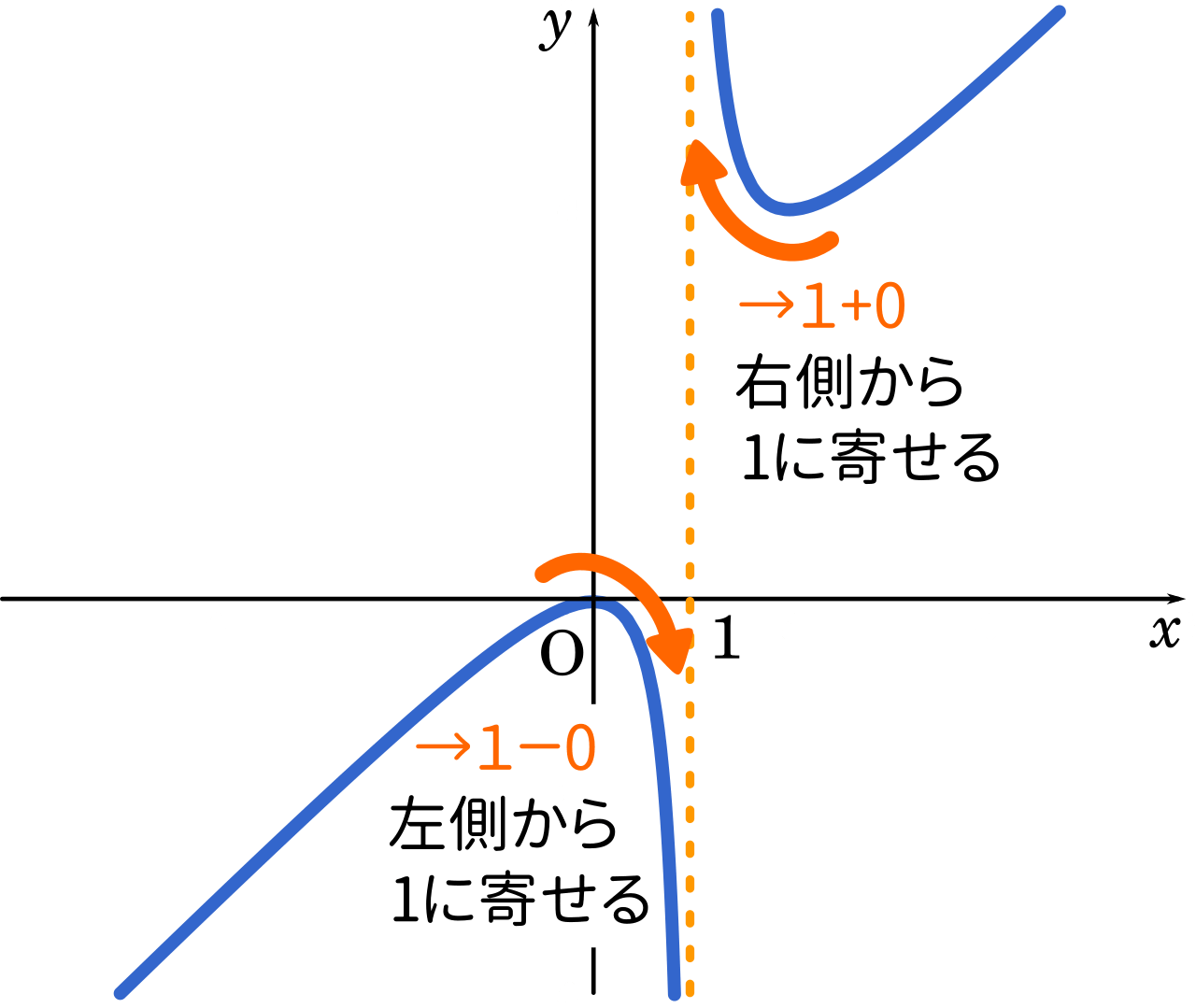
漸近線 有理関数等の水平漸近線,垂直漸近線,斜め漸近線を求める. 関数の漸近線を計算する: (2x^3 4x^2 9)/ (3 x^2) の漸近線 erf (x)の漸近線 方程式で与えられる曲線の漸近線を求める: 漸近線 x^2 y^3 = (x y)^2 もっと表示32 \(y\)軸に平行でない漸近線の求め方2STEP 321 STEP1 \(\frac{f(x)}{x}\)の極限を調べる→傾きチェック; · イメージとしては、 y = tanx y = tan x のグラフと x = π 2 x = π 2 を考えるといいでしょう。 漸近線が x = b x = b となるのは、 lim x→b−0f (x) = ∞, lim x→b−0f (x) = −∞ lim x→b0f (x) = ∞, lim x→b0f (x) = −∞ lim x → b − 0 f ( x) = ∞, lim x → b − 0 f ( x) = − ∞ lim x → b 0 f ( x) = ∞, lim x → b 0 f ( x) = − ∞ の少なくともどれか1つが成り立つときです。




数 関数 分数関数 平行移動 漸近線 オンライン無料塾 ターンナップ Youtube
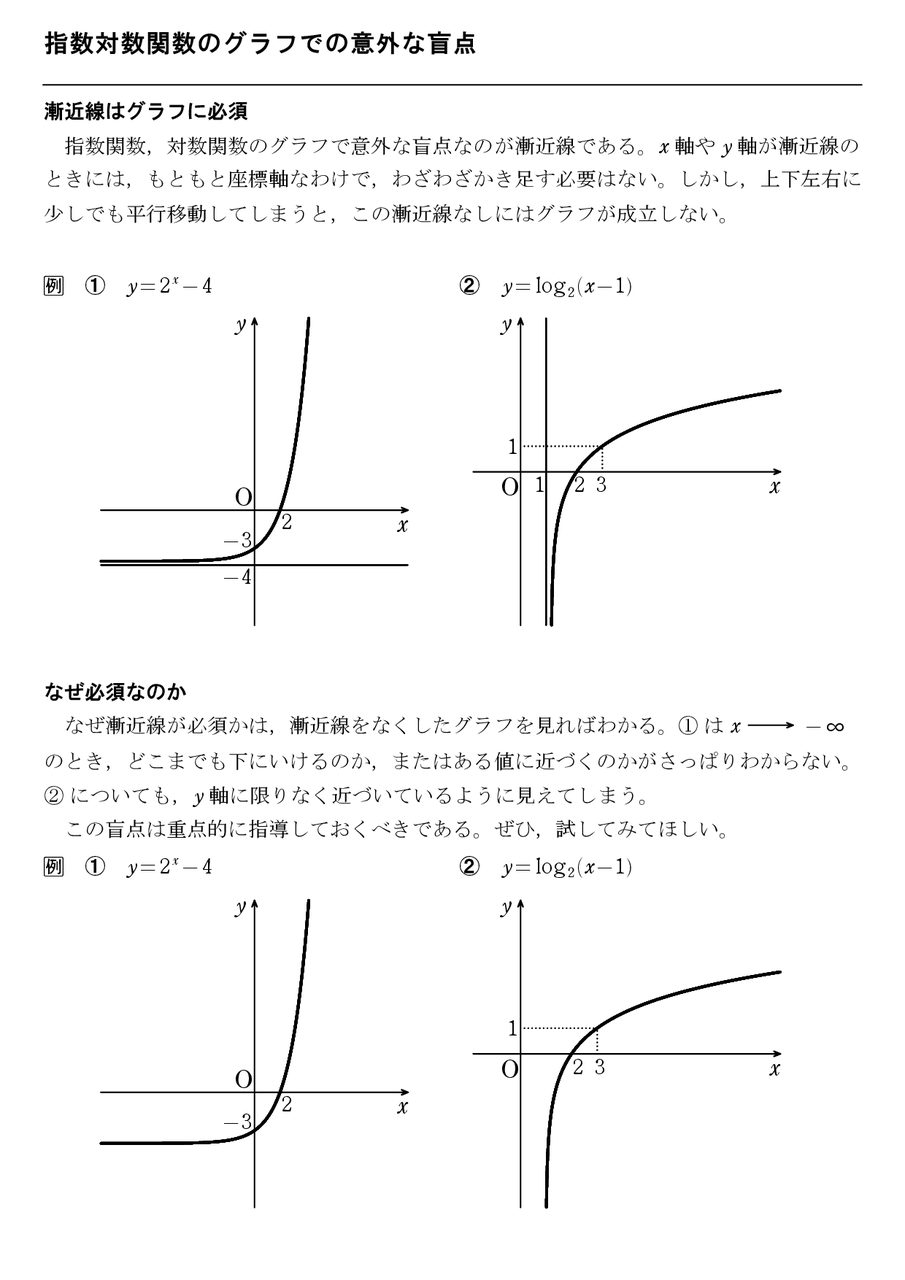



指数対数関数のグラフでの意外な盲点 怜悧玲瓏 高校数学を天空から俯瞰する
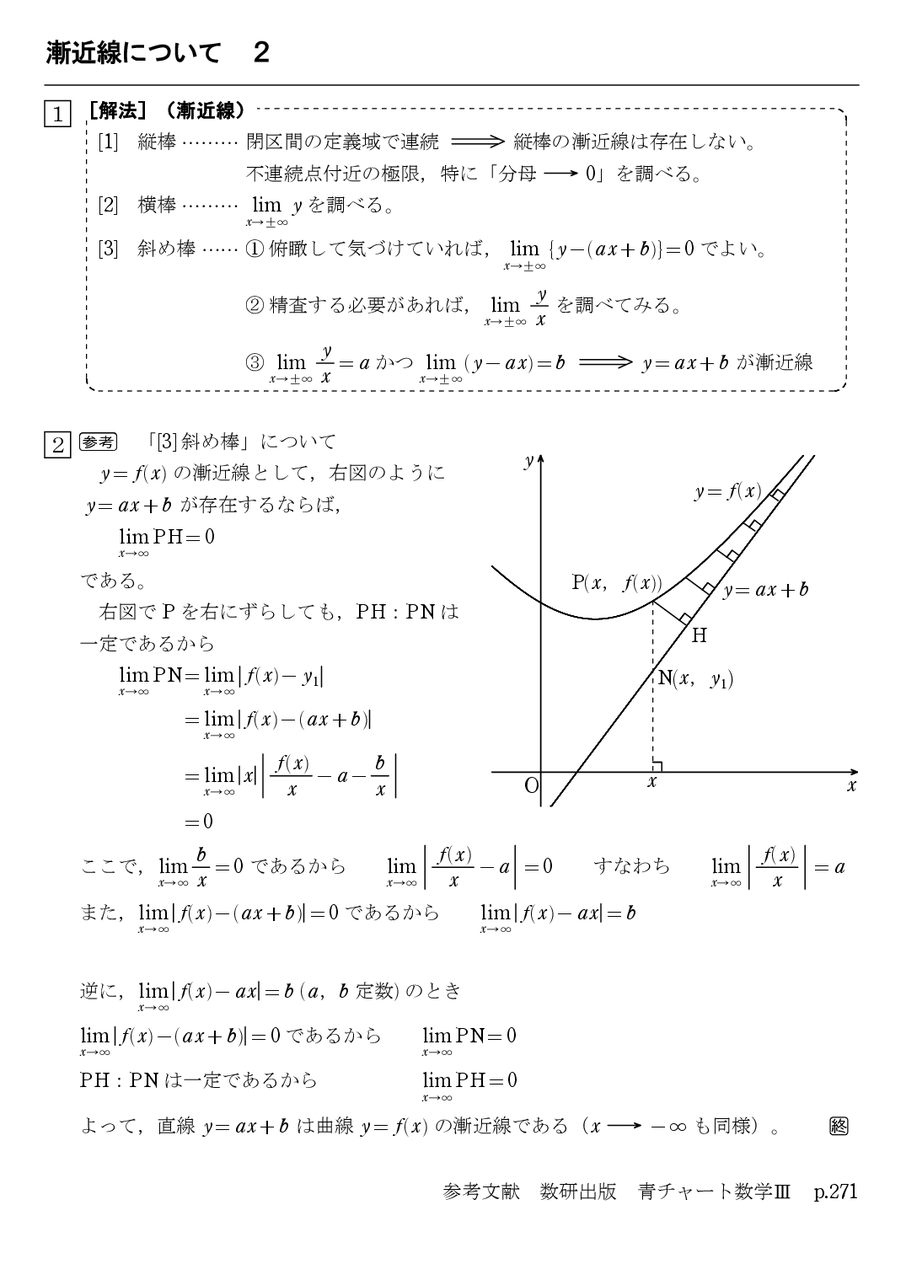
2) 1)の極限値が存在するとき, a の値を用いて, limx→∞limii {f (x)−ax} = b とする. ※ 横 ( x 軸に平行)の漸近線は,直ちに見つかることがあります。 例 y = e −x2 のとき limx→∞limii e −x2 = 0 だから y = 0 は漸近線です. 上の議論で a = 0, b= 0 です。 ※ ( y = ±f (x) のように初めから曲線が2つあるような場合は論外として) 横の漸近線があれば斜めの漸近線はありませ2次関数や3次関数のグラフはだいたいの形が決まっていますが, 複雑な関数のグラフは, 増減だけでは正確な形がわかりません。それでは, 増減のほかに何を調べたらよいか, 具体的な例を見てみましょう。 これより, yの増減表は次のようになります。漸近線の求め方に関する考察 玉 たま 井 い 克 かつ 樹 き 曲線 =f( ) は を媒介変数とする自然な媒介 変数表示 = , =f( ) をもつので,これを利用 して説明する。以下,f( )は定義域で連続である と仮定する。 例えば,直線 =c が曲線 =f( ) の漸近線に なるとする。曲線 =f( ) 上の点P( ,f( ))が 直線




指数関数のグラフのやり方教えてください Clear



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




数3の グラフの凹凸と変曲点を求める問題での漸近線の求め方が あいうえおって何ってい Clear
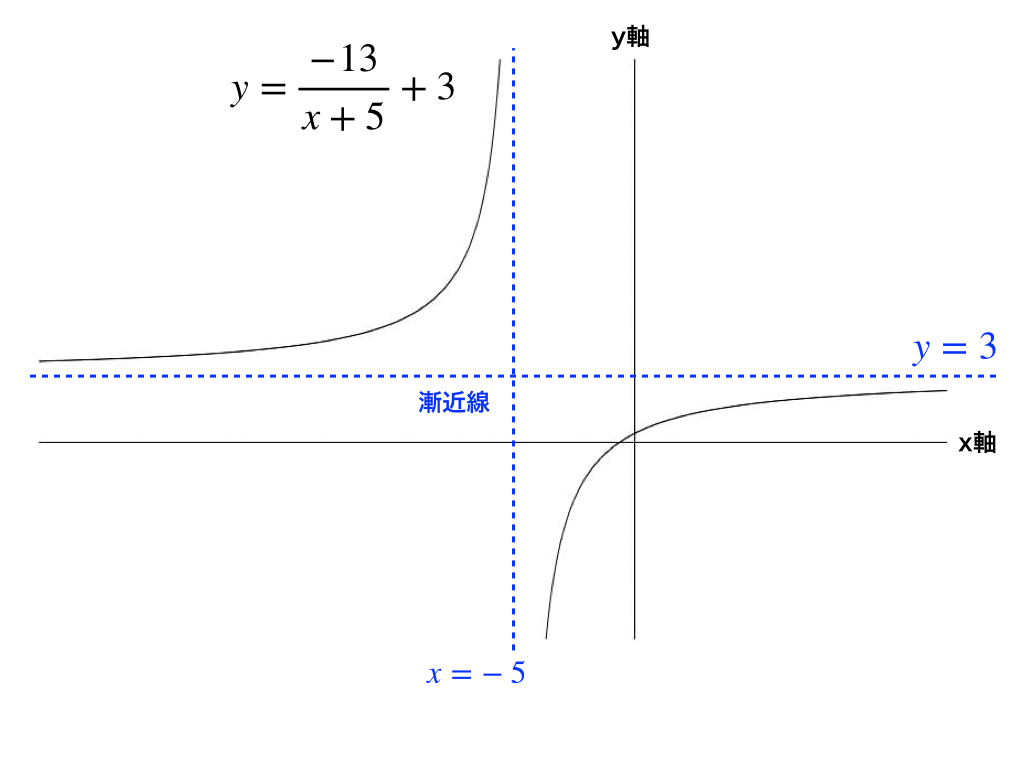



漸近 線 求め 方 漸近線の求め方を解説しました




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




高校数学 2次曲線の決定 2 問題編 映像授業のtry It トライイット



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




数iii Cerca Al Twitter



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




数学3




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線 Wikipedia
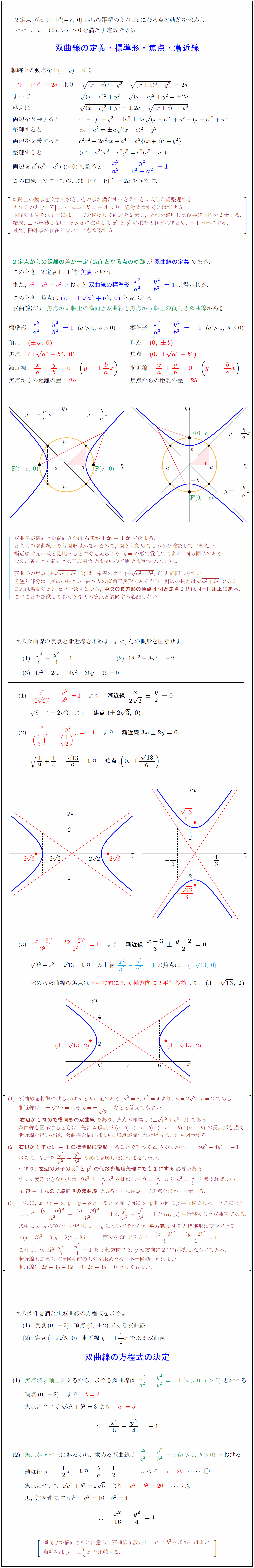



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月




分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




Javascript Y軸に平行な漸近線を描く Mm参考書




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線の求め方が分かりません 3 です Clear




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋
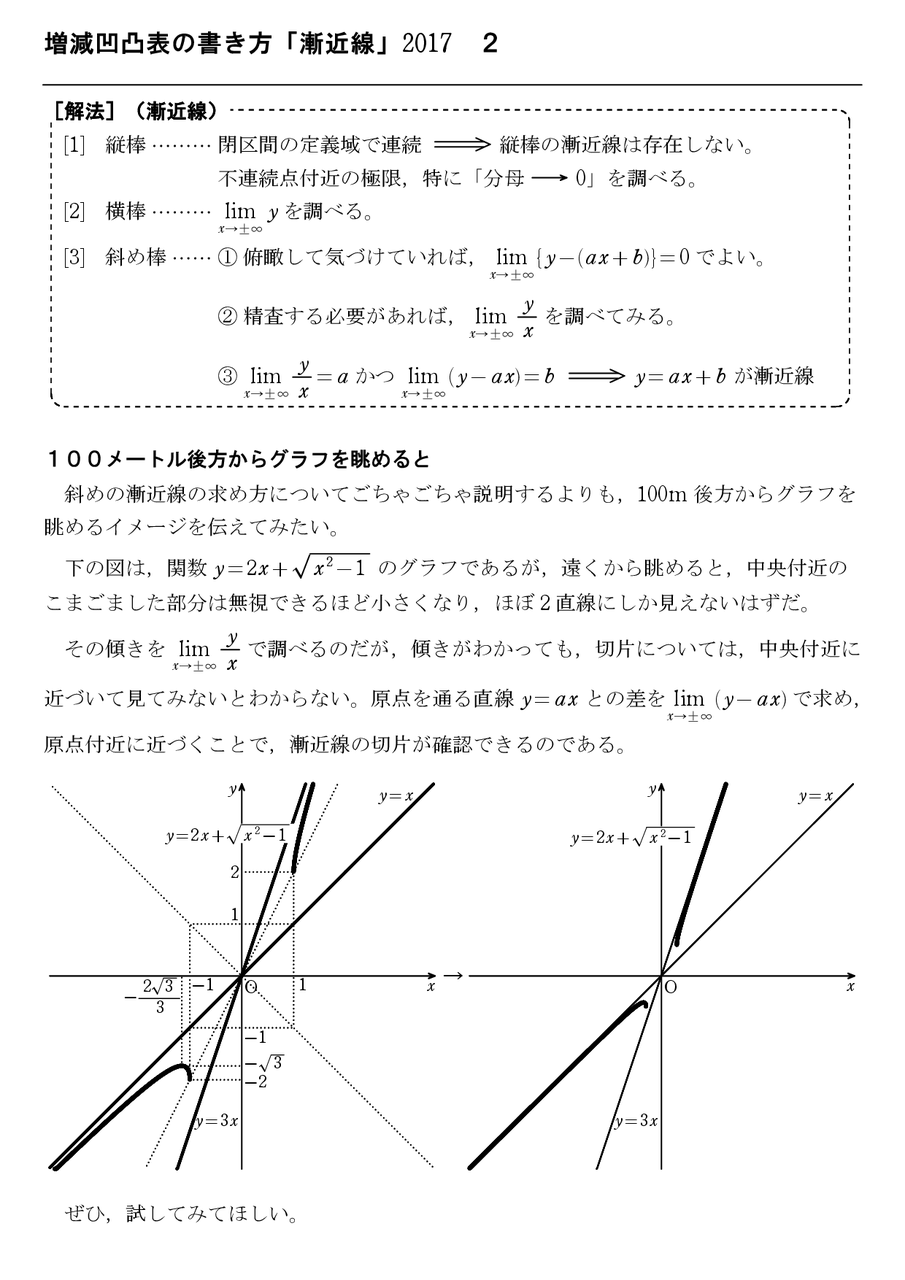



増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する




数学 近似式まとめ 各種公式 求め方 理系ラボ




漸近線 説明編 数 微分法 現大手予備校講師の5分でわかる 高校数学 Youtube



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



数学 微分の質問です これは漸近線を求めていると思うのですが なぜ 漸近線 Yahoo 知恵袋



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




漸近線の求め方 高校数学 微分法の応用 14 Youtube




この漸近線の求め方がわかりません なぜy Xをするのか教えて下さい Clear




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



増減凹凸表を書く手順 7 漸近線 2 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
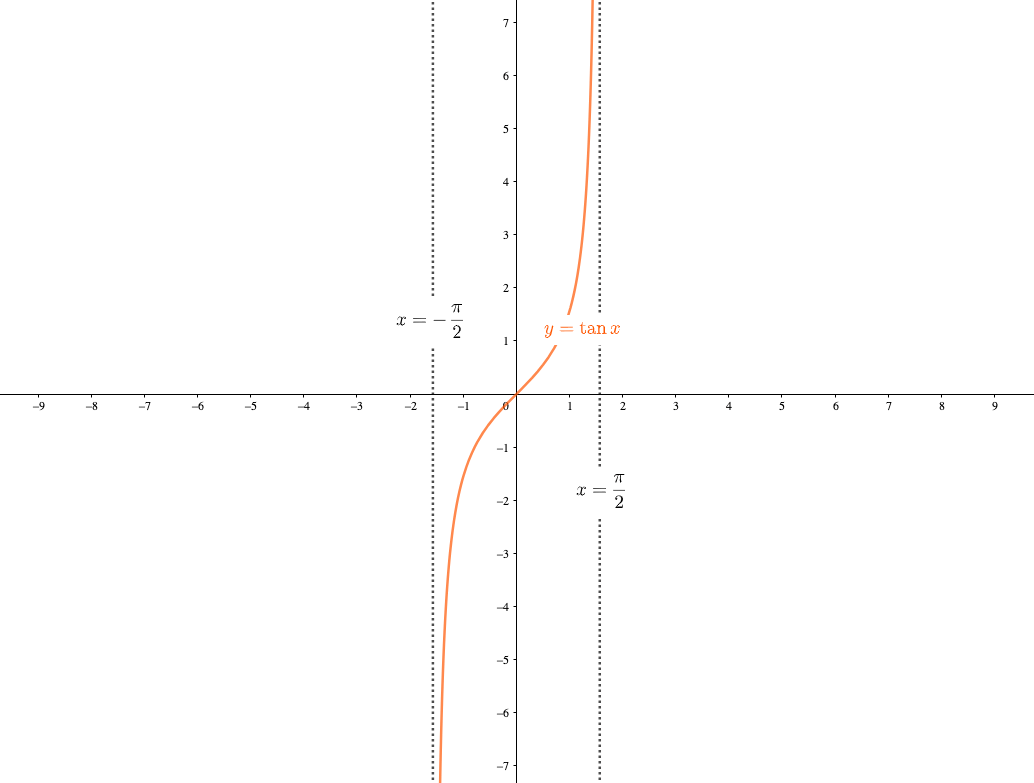



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




増減凹凸表を書く手順 7 漸近線 3 怜悧玲瓏 高校数学を天空から俯瞰する



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




数3の グラフの凹凸と変曲点を求める問題での漸近線の求め方が あいうえおって何ってい Clear




高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット




新入試対応 数学iii基礎問題精講 四訂新装版 上園信武 本 通販 Amazon



漸近線方程




漸近線 英語




数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube



漸近 線 と は 数 微分の応用 ざっくりイメージから漸近線を導く




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




数学3



数3は医学部受験の鍵 勉強の進め方と時期を解説 数3なしの裏技も アガルートメディカル コラム




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




次の曲線について 放物線なら頂点の座標 権円なら中心の座標 双曲線なら漸近 クァンダ Qanda で解き方を見る




高校数学 漸近線の求め方 前編 増減表で自動化 タテ ヨコ 予想法 Youtube
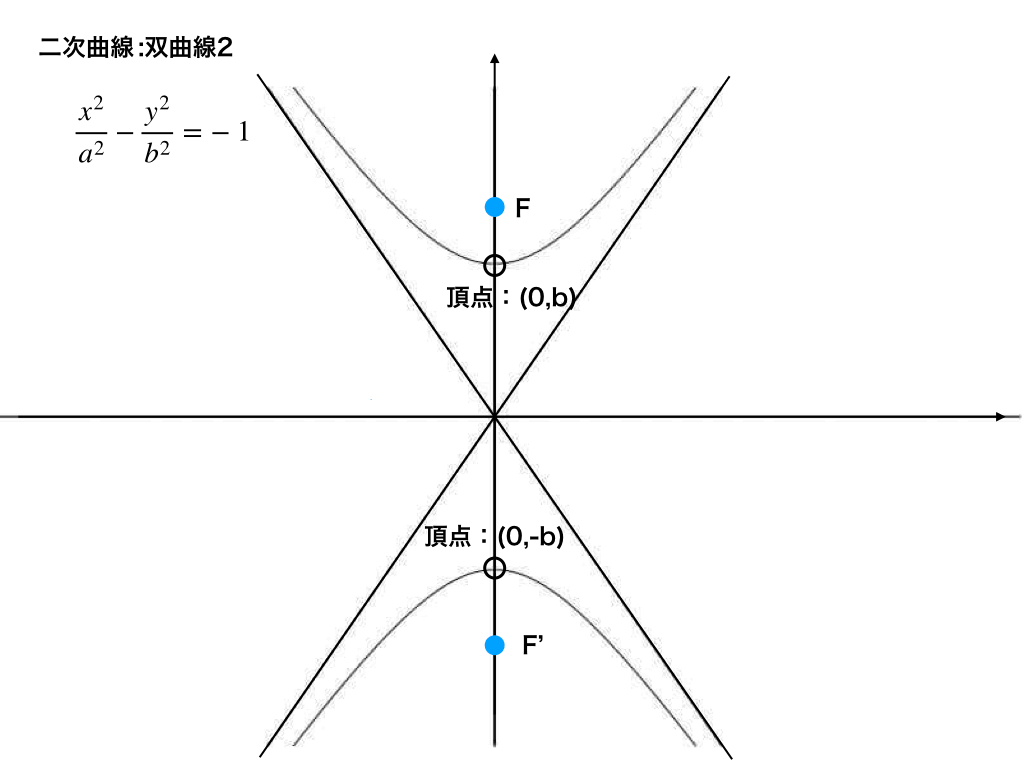



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説
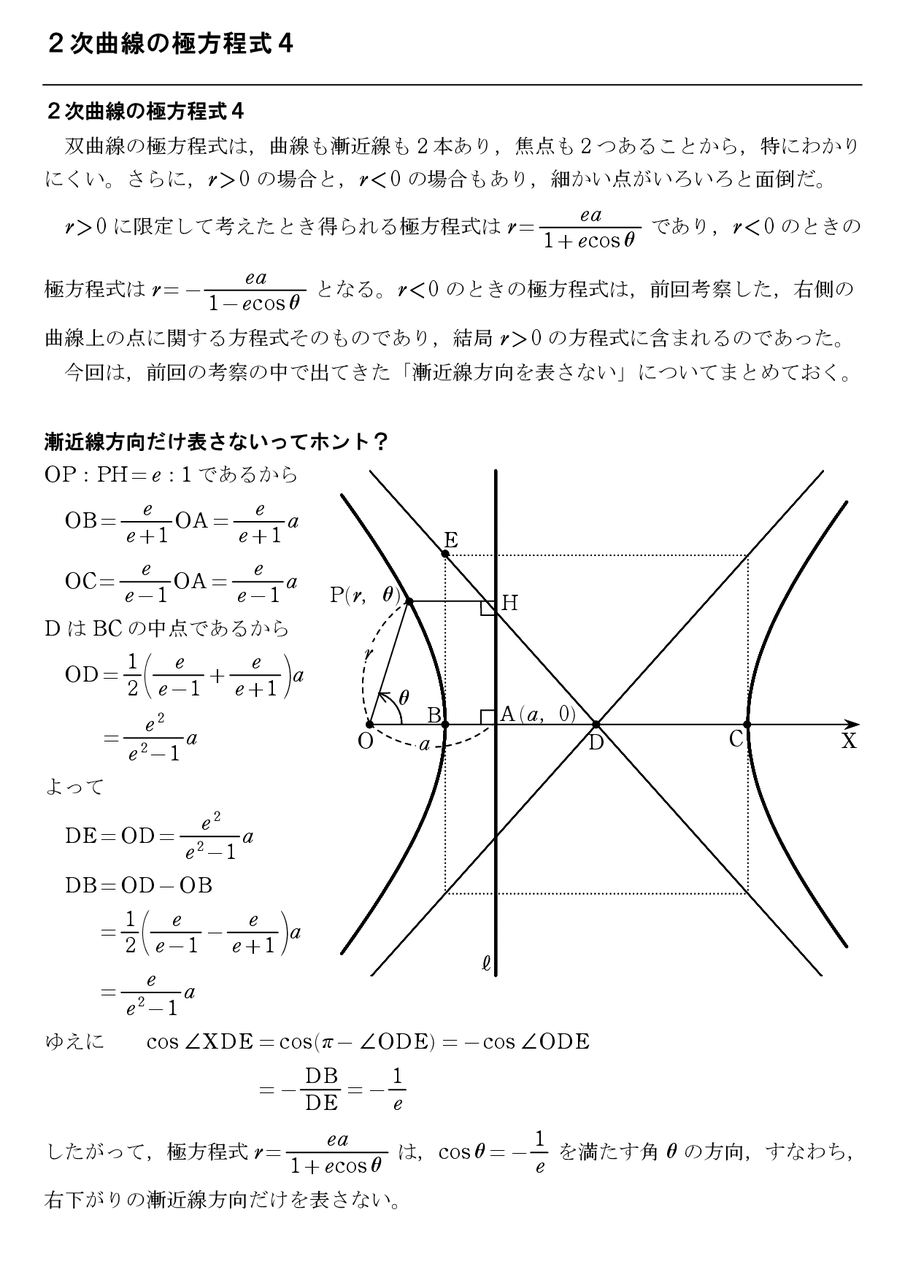



2次曲線の極方程式4 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線
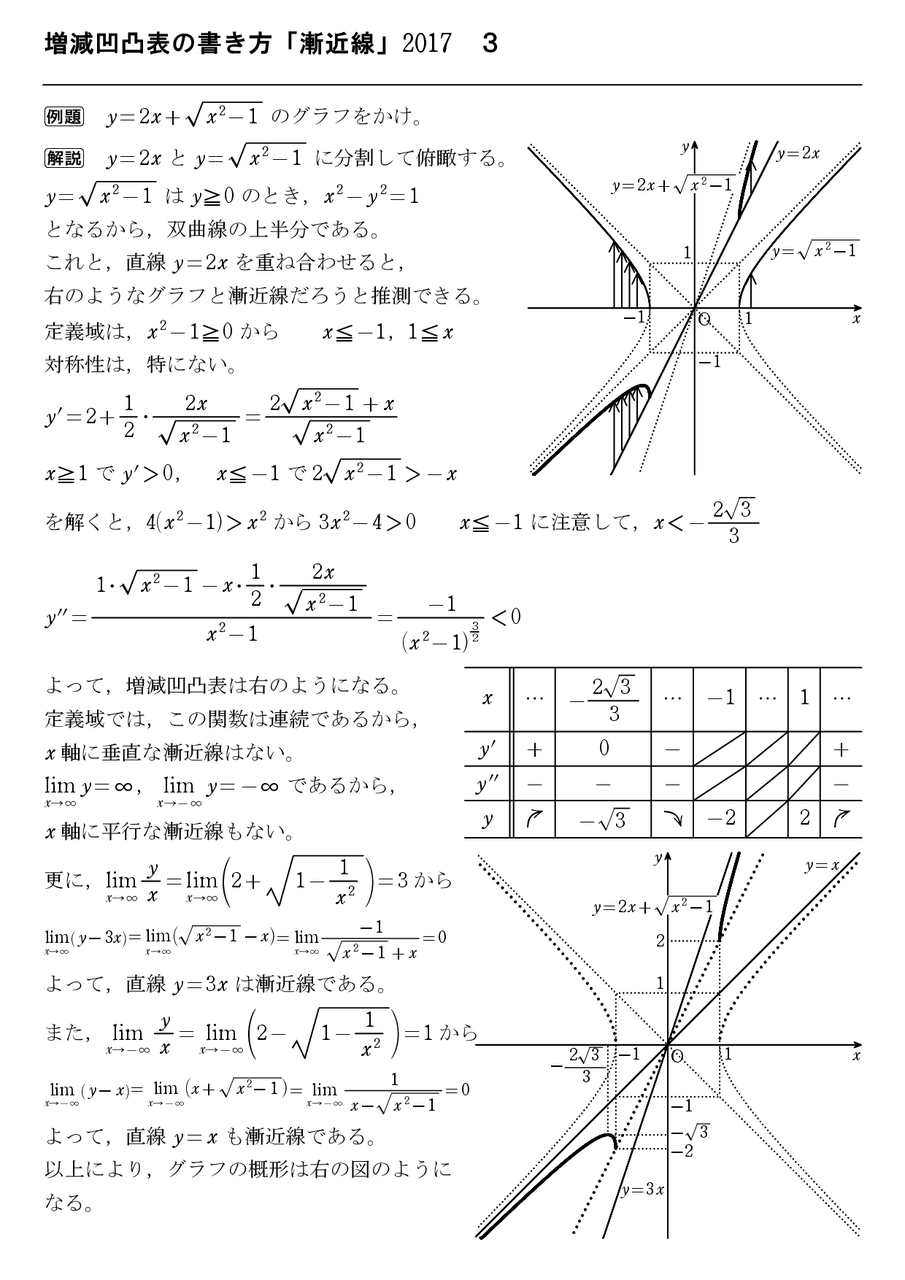



増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する
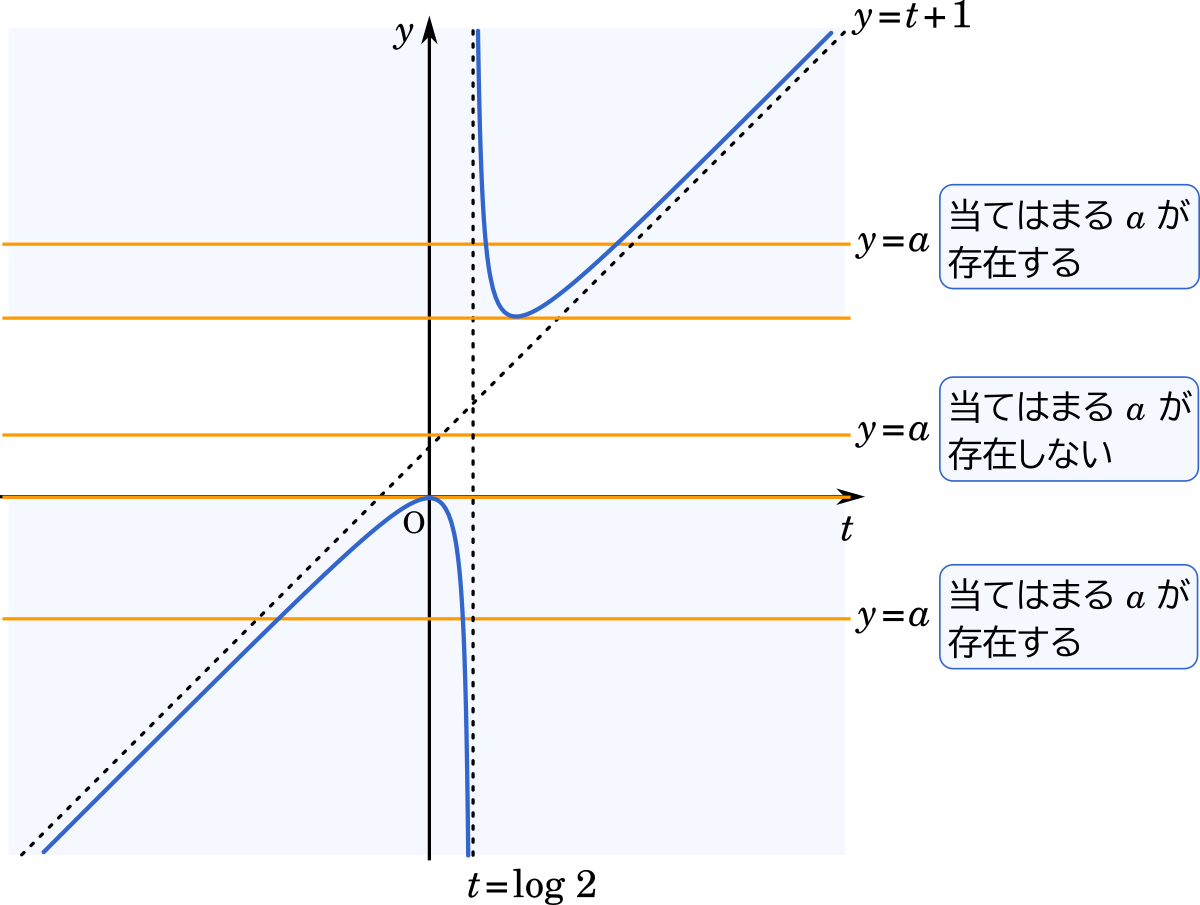



数iii微分 接線の座標の存在範囲 漸近線を求めてグラフの概形を描く 九州大 Mm参考書



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




分数関数の問題です 3 いつもお世話になっております 分数関数を Okwave
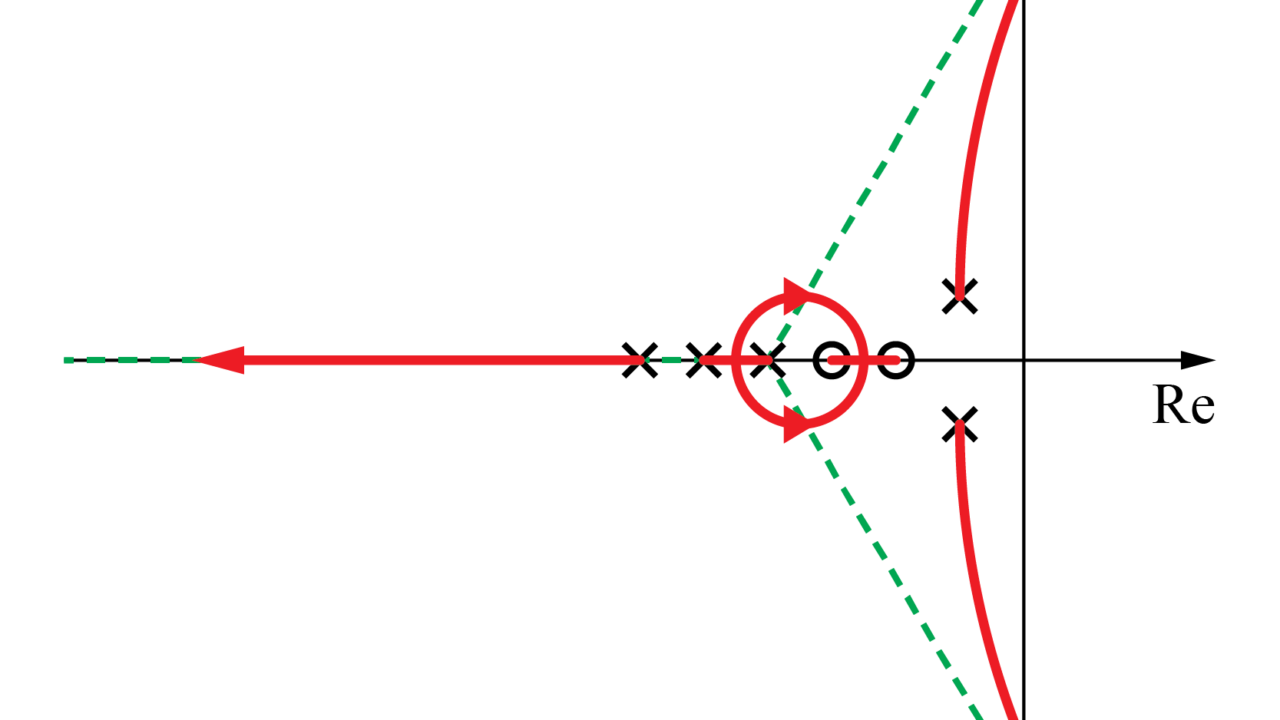



複雑なフィードバックシステムの根軌跡を詳細に描く Tajima Robotics




Y Ax B 2x 1 1 のグラフが点 1 0 Okwave




双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説
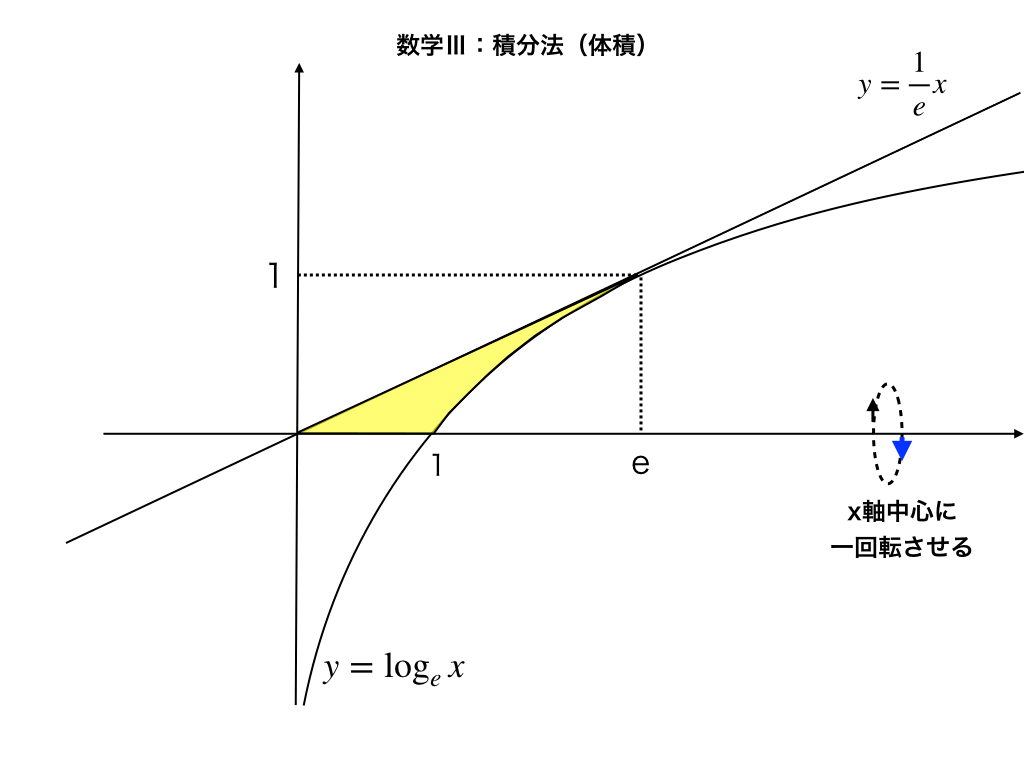



関数のグラフと接線が囲む面積 体積を求める問題をわかりやすく解説



Y Logx 2 Descubre Como Resolverlo En Qanda
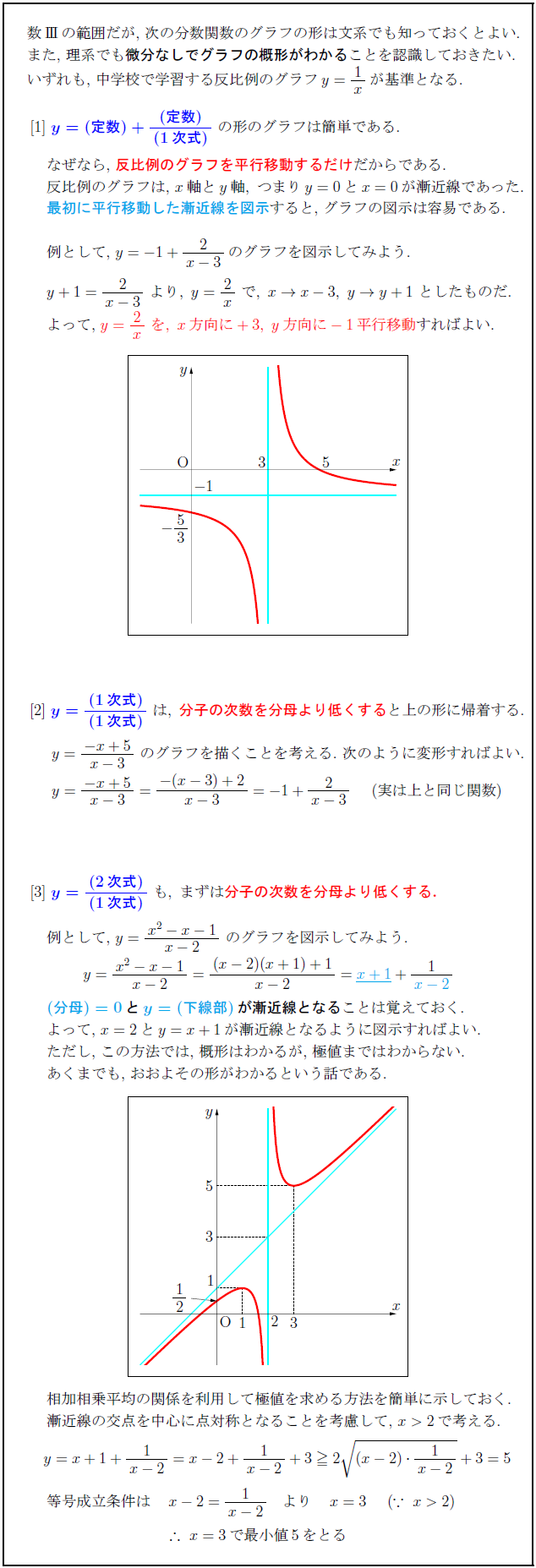



高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月




メャン 1414canf Twitter




高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどういう意味な Clear



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典
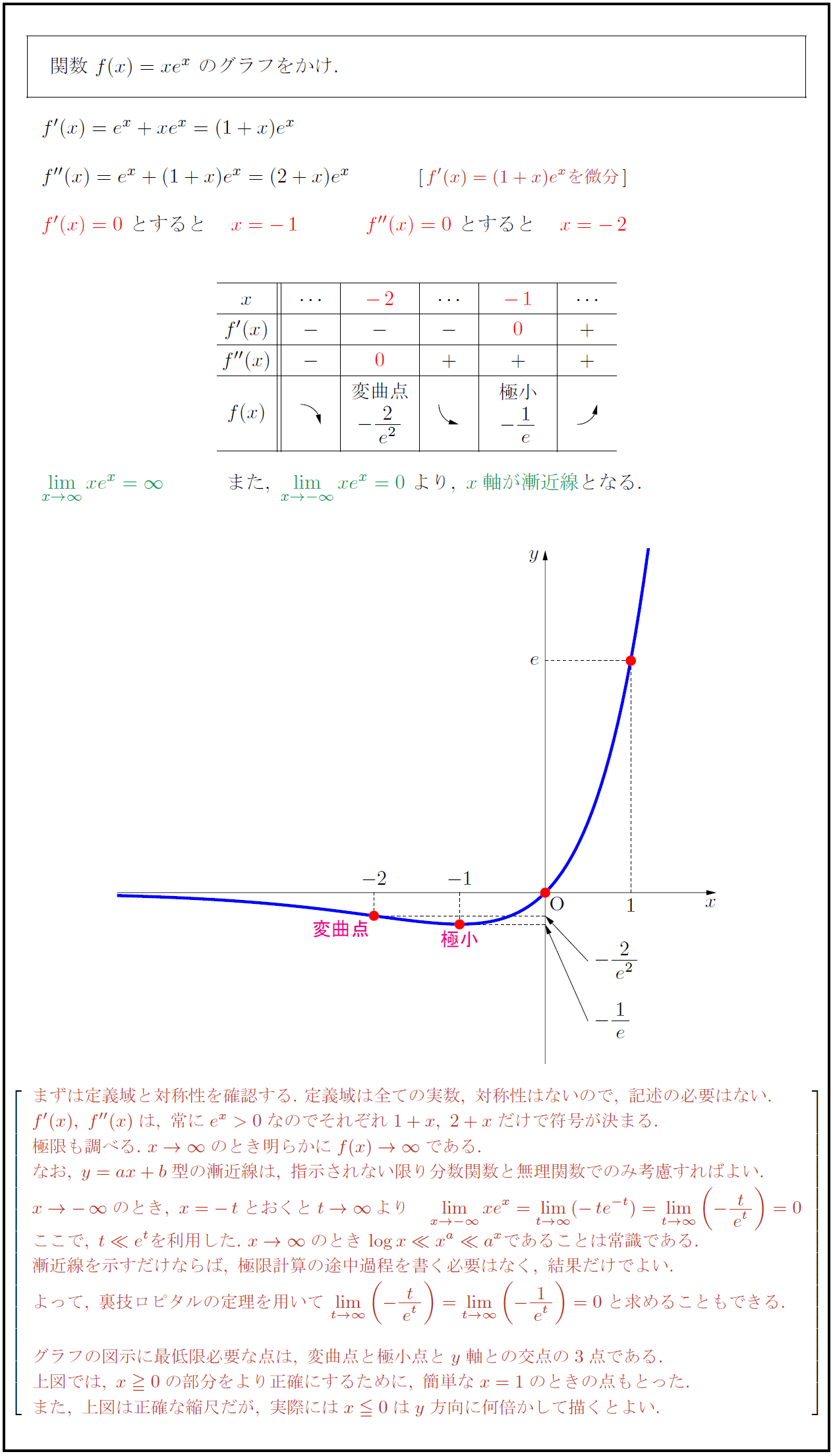



高校数学 指数関数 Y Xe X のグラフ 受験の月




漸近線方程



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




高校数学 2次曲線の決定 2 問題編 映像授業のtry It トライイット




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



分数関数のグラフ 反比例と平行移動 高校数学の知識庫



0 件のコメント:
コメントを投稿